Mind Map: The Bluffers Guide To Networks

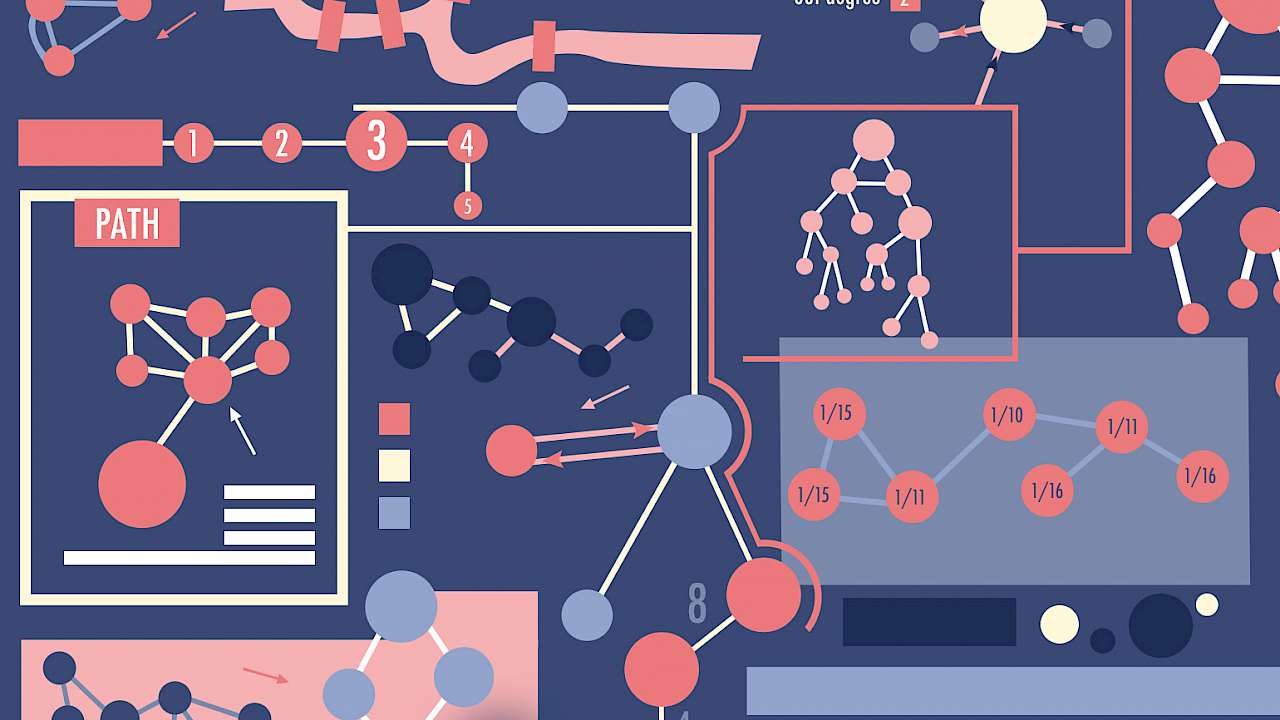
When it comes to network analysis the technical terms and lingo used to describe the different elements and structures that make up a network can be confusing. That's why we've created this handy guide that breaks down the jargon, so if you can tell your nodes from your ties ...

Node

The nodes (also known as ‘actors’ and ‘vertices’) are the people or entities that make up the members of the network. They can be individuals, or also organisations, sub-teams, roles or even pieces of technology. Whatever they are, they are the ‘blobs’ or ‘dots’ in a network diagram. So, in the expression “Suspect A provides a tasking to Suspect B” we have two nodes (persons A and B) and a relationship (‘provides tasking’) that connects the two.

Tie / Edge

The connections or relationships between nodes are called ‘ties’ or ‘edges’. A tie suggests a connection of some sort between two nodes.

Multi-directional ties

Some ties have arrows showing the direction of a connection. So, if person A sends instructions to person B, that tie would have an arrow pointing from A to B. If B returns something back, there’s another tie, with an arrow in the opposite direction.

Uni-directional ties

If there’s no direction in a tie it is uni-directional. For instance, if the ties are kinship-based, then there would be a single link, with no arrows. Or if a connection is reciprocal – for instance, Facebook or LinkedIn connections, compared to, say, Twitter, when A can follow B, but B does not need to follow A.

Weights

A tie can be weighted or unweighted. If it’s weighted, it has a numerical value that represents the strength or frequency of a connection (number of messages exchanged, closeness of relationship).

Node degree

The number of connections coming into a node (in-degree) and out of a node (out-degree). Degree centrality is the number of connections a node has – it is a simple measure of influence, but having more connections doesn’t always mean someone is more influential.

Graph theory

The mathematics behind a ‘graph’ that contains nodes (‘vertices’) and ties (‘edges’). Graph theory describes how a network is drawn, as well as how the structure of the network can be expressed mathematically.

Bridges of Königsberg

The original problem, how to cross the bridges once and only once, that led mathematician Euler to publish the first paper on graph theory in 1736.

Path

If you imagine a network made up of nodes and edges, the ‘path’ is the route between any two nodes. So, If Ted is connected to Sam who connects to Georgina, then a path would be from Ted -> Sam -> Georgina.

Distance

‘Distance’ is the number of nodes and edges that are traversed to reach from one point to another. It is a reasonable proxy for how much potential influence a person might have in a network – if they have to cover a considerable distance to reach most other nodes, their reach and influence is likely to be less than a person with easier access to the rest of the network.

Bridge / Boundary spanner

A node that connects two or more nodes/subsets of nodes that would be disconnected otherwise. A lack of a bridge creates a ‘structural hole’ within a network.

Structural hole

An area within a network where there are no ties between nodes. Structural holes can be exploited by ‘boundary spanners’ (or entrepreneurs) to create value by identifying complementary ideas or products and connecting them.

Betweenness centrality

A measure that expresses the likelihood of a node being a ‘bridge’ or ‘boundary spanner’. For instance, if a terrorist cell has six closely connected members, but only one has a connection to the wider network, that one person would score higher in betweenness centrality.

Closeness centrality

A score that expresses the average distance of a single point to reach all other points in a network (or graph). A higher score means that the node is ‘closer’ to the rest of the network – meaning that they have a better sight of the overall network.

Density

The degree to which all nodes are connected to each other. A densely connected network will be more resilient to the removal of nodes (and their edges) since other routes exist to connect up.

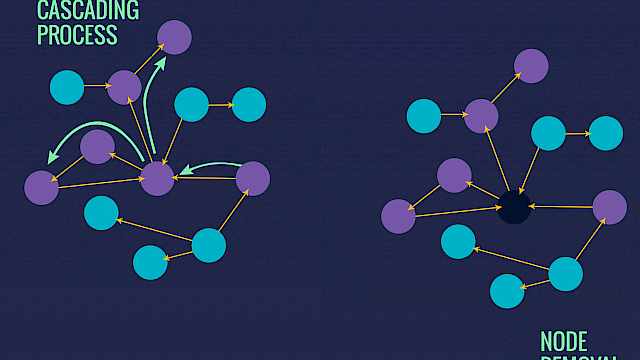
Cascades

The term used to describe how information spreads across a network (e.g. news, rumour, pattern of behaviour). The ‘seed’ node is the originator of the information, and if their connections propagate to their connections (or copy the behaviour), and then their contacts do the same, then a ‘cascade’ has begun.